Dynamic programming 개념을 설명할 때 피보나치 수열 말고도 가장 흔하게 언급되는 예시가
배낭 문제(knapsack problem)이다.

어느 정도 난이도가 있는 배낭 문제는 DP로 푸는 게 대부분이다.
배낭 문제를 처음 접해본 사람은 올바른 풀이를 떠올리기 정말 어렵다.
그러나 배낭 문제는 결국 사소한 문제 설정에서 차이가 있을 뿐 비슷한 유형의 문제를 풀다보면 동일한 패턴을 발견하게 된다.
결국 배낭 문제는 풀이 방식이 비슷하기 때문에 아예 풀이를 외울 정도까지 익숙해지는 게 좋다고 생각한다.
배낭 문제에 속하는 예시 몇 가지를 아래에서 살펴보자.
백준 7579번: 앱

문제 설정은 앞서 살펴본 11066번(파일 합치기)와 11049번(행렬 곱셈 순서)와는 다르다.
이전 문제는 어떤 연속된 값을 모두 선택해서 하나의 값으로 만드는 과정이었다면
이 문제에선 어떤 값을 고르는 개수와 순서와 상관없이 선택해서 합한 결과가 특정한 값 이상이어야 한다는 조건이 있다.
그리고 또 한 가지 특징이 있다.
배낭 문제에서는 한 항이 두 가지 값을 가진다. 하나는 물건의 무게이고, 다른 하나는 물건의 가치다.
이 문제에선 물건의 무게가 '활성 메모리', 가치는 '비활성화 후 다시 활성화하는 데 드는 추가 비용'이라고 볼 수 있다.
오리지널 배낭 문제와 이 문제의 차이점은 다음과 같다.
- 배낭 문제에선 배낭이 담을 수 있는 최대 무게 W가 정해져 있어 무게의 합이 W 이하가 되도록 하되 가치 합을 최대로 만든다.
- 현재 문제는 활성 메모리 합이 M 이상이 되도록 하되 추가 비용 합을 최소로 만든다.

DP 배열의 설정
사실 배낭 문제는 dp 배열을 어떻게 설정할지 올바르게 결정한다면 절반은 푼 셈이라고 생각한다.
dp 배열은 다음과 같이 설계되어야 한다.
dp[n][c] = V : 0번째부터 n번째 항 중에서 골랐을 때, 추가 비용의 합을 c 이상으로 하여 만들 수 있는 메모리 합의 최댓값은 V이다.
memories = [0] + list(map(int, input().split()))
costs = [0] + list(map(int, input().split()))
N = len(memories)
dp = [[0 for _ in range(sum(costs)+1)] for _ in range(N+1)]
1. '0번째부터 n번째 항 중에서 골랐을 때'라는 말은 즉 0번째부터 n번째 항을 모두 합했다는 뜻이 아니라,
일부(또는 문제 설정에 따라 전체일 수도 있다)만 선택한다는 뜻이다.
2. dp 배열은 2차원이고, 두 번째 차원의 크기는 추가 비용(배낭 문제에선 물건의 가치 총 합)의 총합이어야 한다.
'이상' vs. '만큼'
dp[n][c] = V : 0번째부터 n번째 항 중에서 골랐을 때, 추가 비용의 합을 c 이상으로 하여 만들 수 있는 메모리 합의 최댓값은 V이다.
dp[n][c] 에서 c는 비용을 c 이상 들였을 때 만들 수 있는 메모리 합의 최댓값이다.
예를 들어 dp[2]를 업데이트하고 있다고 가정하자.
0~2번째 항을 모두 선택하면 비용 합이 6이고, 이는 0~2번째 항을 가지고 만들 수 있는 비용의 최대값이다.
이 때 메모리 합은 60이다.
문제에서 주어진 총 비용 합은 15이므로, dp[2][6] ~ dp[2][15]은 모두 값이 60이 들어가게 된다.
다시 말하자면 0~2번째 항만을 가지고 만들 수 있는 비용 최대값이 해봤자 6이니
비용을 7,8,... 으로 더 늘린다고 해도 얻을 수 있는 메모리 최대 합은 60으로 일정한 것이다.
배낭 문제에선 dp 배열에 정확한 값이 아니라 누적된 값을 대입한다는 사실을 명심하자.


풀이
N, M = map(int, input().split())
memories = [0] + list(map(int, input().split()))
costs = [0] + list(map(int, input().split()))
sum_costs = sum(costs)
dp = [[0 for _ in range(sum(costs)+1)] for _ in range(N+1)]
for i in range(1, N+1):
mem, cost = memories[i], costs[i]
for c in range(1, sum_costs+1):
if c < cost:
dp[i][c] = dp[i-1][c]
else:
dp[i][c] = max(mem+dp[i-1][c-cost], dp[i-1][c])
for i in range(sum_costs+1):
if dp[-1][i] >= M:
print(i)
break
백준 2629번: 양팔저울
이 문제도 결국 배낭 문제와 살짝 설정만 다를 뿐 접근 방식은 동일하다.
차이점은 다음과 같다.
- 배낭 문제에선 물건 무게 합의 최소(7579번(앱)에선 메모리 합의 최대)를 구했다면, 이 문제에선 특정 무게를 만들 수 있는지 가능 여부(True or False)를 따진다.
- 배낭 문제에선 기존 무게 합에 현재 물건의 무게를 더해나갔다면, 이 문제에선 기존 가능한 무게에 대해 1) 현재 추의 무게를 더하거나 2) 현재 추의 무게에서 가능한 기존 무게 합을 빼거나 3) 기존 무게 합에서 현재 추의 무게를 빼서 가능한 무게의 가짓수를 구한다.
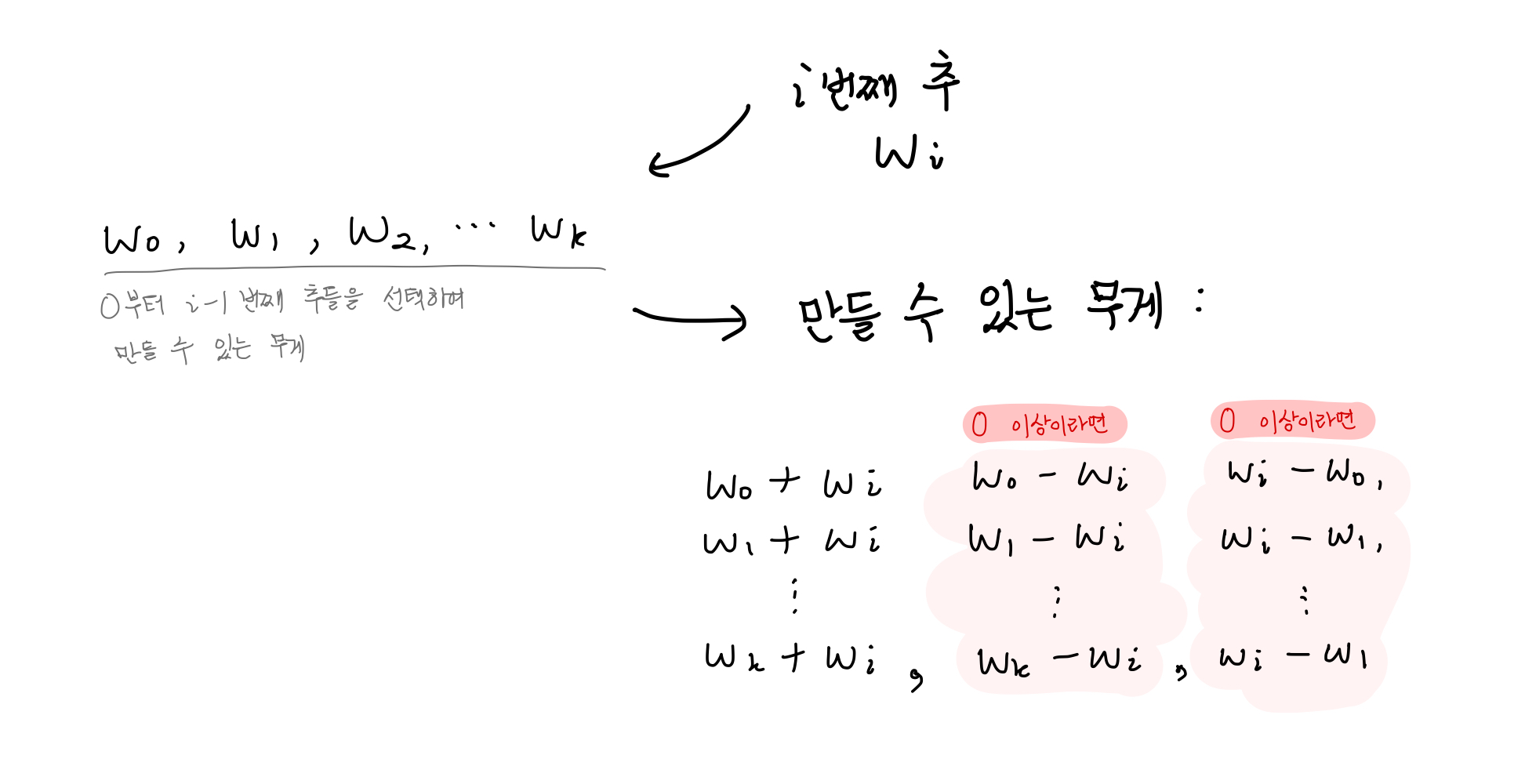
DP 배열의 설정
dp = [[False]*(sum_weights+1) for _ in range(N_weight)]
dp[0][0] = True
dp[0][weights[0]] = True
배낭 문제와 마찬가지로 추의 개수를 dp 배열 1차원의 크기, 추 무게의 총합을 2차원의 크기로 정했다.
점화식
acc_sum = weights[0]
for i in range(1, N_weight):
cur_w = weights[i]
for w in range(acc_sum+1):
if dp[i-1][w]:
dp[i][w] = True
dp[i][w+cur_w] = True
if w - cur_w >= 0:
dp[i][w - cur_w] = True
if cur_w - w >= 0:
dp[i][cur_w - w] = True
acc_sum += cur_w
- N_weight는 추의 개수이고, acc_sum은 추의 무게의 누적 합을 의미한다.
- 위 반복문을 수행하고 나면 dp[-1]에는 0부터 N-1번째 추들을 사용하여 만들 수 있는 무게에 대한 정보(True / False)가 모두 저장된다.
그럼 아래처럼 dp 배열의 무게 합이 구슬 무게와 일치할 때만 'Y'를 출력하면 될까?
answer = []
for marble_weight in marbles:
if dp[-1][marble_weight]:
answer.append('Y')
else:
answer.append('N')
print(' '.join(answer))
dp 배열의 2번째 차원 크기는 추의 무게 총합으로 정했을 뿐, 구슬 무게와는 상관없다.
즉 한 구슬 무게가 전체 추의 무게 총합보다 클 수도 있다는 뜻이다.
이런 입력이 주어진다면 dp 배열을 참조할 때 IndexError가 발생하게 된다.
수정한 코드
answer = []
for marble in marbles:
if marble > sum_weights:
answer.append('N')
else:
if dp[-1][marble]:
answer.append('Y')
else:
answer.append('N')
print(' '.join(answer))
항상 예외 케이스를 먼저 신경 쓰고 처리하는 습관을 들이자.
