Dynamic Programming(DP) 개념을 처음 소개할 때 빠지지 않고 등장하는 게 피보나치 수열이다.
설명 글을 요악하면 다음과 같다.
1) 피보나치 수열을 재귀함수를 이용해 구한다.
2) 재귀함수로 구할 때 중복된 계산이 발생한다. 어차피 같은 답을 내놓는 연산을 여러 번 반복하니 불필요하고 비효율적이다.
3) 불필요한 연산을 방지하기 위해 memoization, 즉 DP 개념을 도입한다.

여기에 핵심이 있다. 우리는 같은 DP 문제에 대해 재귀로 풀 수도 있고, DP로도 풀 수 있다.
이유는 애초에 DP 문제가 다음 성질을 지니기 때문이다.
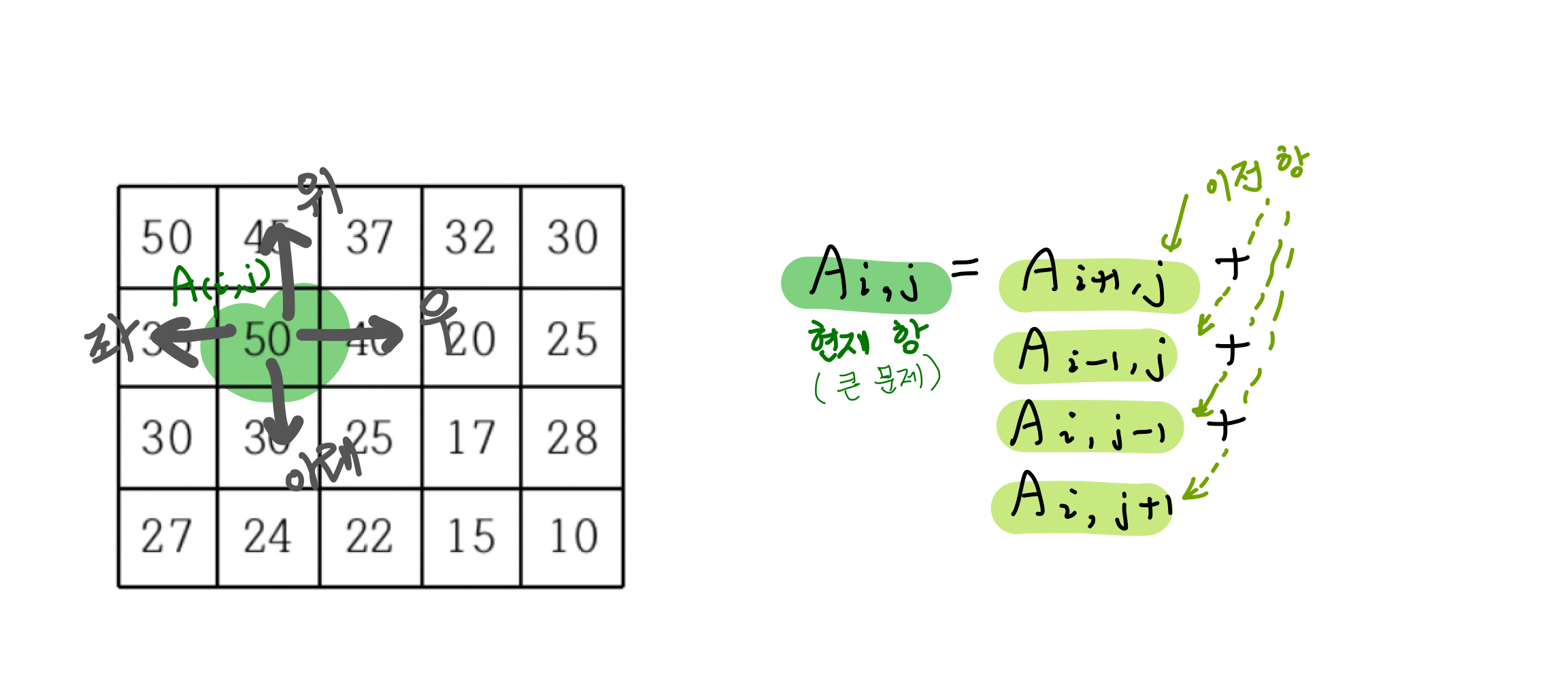
1) 큰 문제(마지막 항, f(n), 구하고자 하는 답, 현재 상태)를 작은 문제(초기값, 이전 상태, 직전 단계)에 의존하는 관계식으로 표현할 수 있다.
2) 여러 번 과정을 반복해도 작은 문제의 결과값은 일정해야 한다.
3) 재귀를 이용하면 동일한 작은 문제에 대한 답을 중복해서 구하는 반면 DP는 이 작은 문제에 대한 답을 저장(memoization 메모이제이션)해서 재사용한다.
dynamic programming과 재귀의 관계
DP 문제의 핵심은 현재 상태와 이전 상태의 관계식(점화식)을 찾는 것이다.
점화식을 컴퓨터의 언어로 표현하면 재귀로 간결하게 나타낼 수 있다.

DP 문제를 바라보는 2가지 방식: Top-Down vs. Bottom-Up
어떤 문제는 처음부터 DP 방식으로 풀려고 하면 도저히 답이 안 나올 때가 있다.
여기서 DP 방식이란 첫번째 항(초기값) A(0)부터 시작해서 A(1), A(2)... 그리고 A(n)까지 순차적으로 구하는 절차를 말한다.
결국 도저히 안 풀려서 나중에 해설 풀이를 보면 재귀를 활용해서 간단하게 풀어내는 경우가 대부분이었다.
문제를 풀 수 있는 방식은 다양하지만(그리고 다양한 풀이를 시도해보는 것도 좋지만)
어떤 문제는 애초에 조건이 top-down 방식으로 설계되었기 때문에, 재귀를 이용해서 푸는 게 훨씬 이해하기 쉽고 직관적이다.
물론 이 문제도 bottom-up (작은 문제를 합쳐 최종 항까지 순차적으로 구하는 정직한 방식)으로 풀 수 있지만
내 경험상 대부분 문제를 top-down으로 풀고 나서야 bottom-up 풀이를 쉽게 떠올릴 수 있었다.

DP 문제를 top-down 방식으로 접근하는 연습을 하자
우리는 bottom-up 방식에는 이미 충분히 익숙해져 있다.
bottom-up은 완전탐색의 원형이기도 하다. 완전 탐색이 곧 처음 항부터 끝 항까지 차례대로 훑어보는 과정을 말하기 때문이다.
또 쉬운 난이도의 DP 문제는 대부분 bottom-up 방식으로 풀린다.
반면 DP 문제를 top-down 방식으로 바라보는 데에는 익숙하지 않을 수 있다.
어떤 문제는 bottom-up으로만 풀겠다는 편견을 버리고 top-down, 즉 처음부터 답을 구했다고 가정하고 더 작은 항으로 쪼개나가는 방식으로 문제를 바라보면 금방 답이 보이기도 한다. 아래에선 그러한 문제를 살펴보기로 한다.
백준 11066번: 파일 합치기
본격적으로 개념 설명을 하기 전에 알고리즘 문제 풀이에 꼼꼼히 읽는 습관이 얼마나 중요한지 다시 한 번 명심하자.
소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고...
각 수열이 연속이 되도록 파일을 합쳐서 최종 파일 하나를 만드는 문제다. 연속 조건이 없었다면 그냥 정렬해서 쉽게 풀 수 있다.
처음에 독해를 설렁설렁해서 저렇게 푼 사람(나도 그랬고...)이 꽤 있었을 거라 예상한다.
top-down 방식
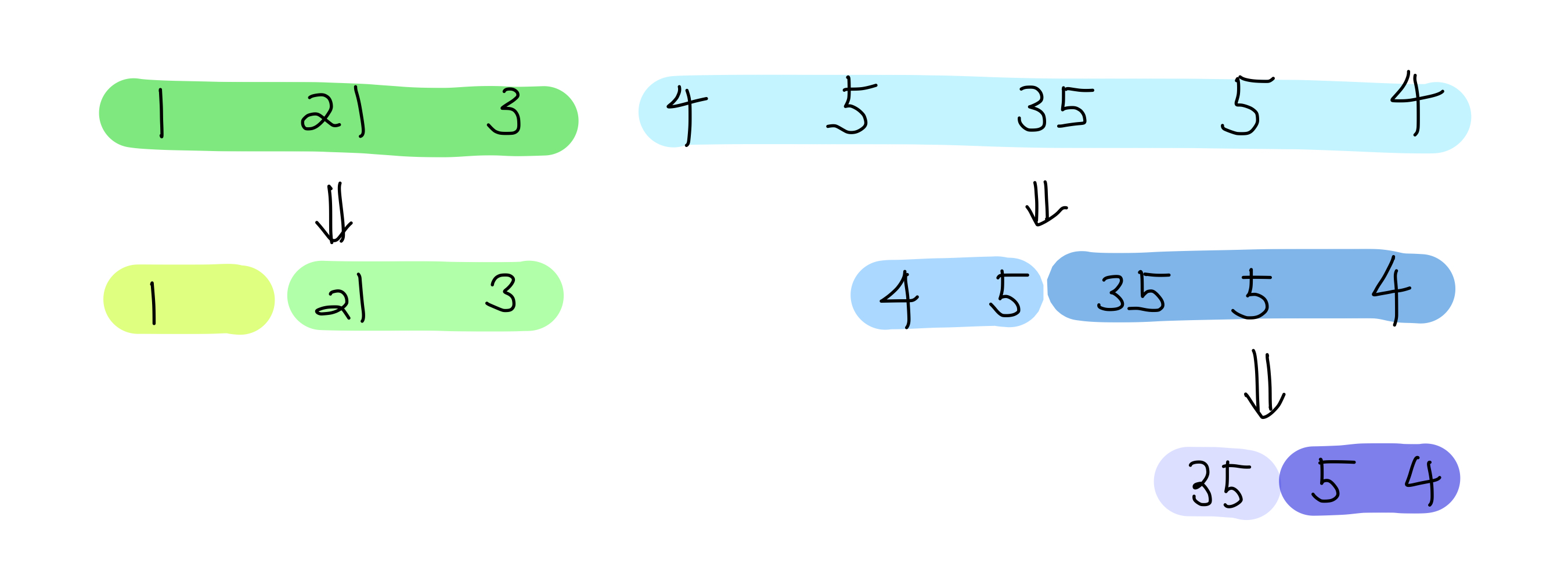
어떤 수열 1, 21, 3, 4, 5, 35, 5, 4가 주어졌다고 해보자.
그리고 답을 이미 구했다고 가정하자. 답은 적어도 아래 그림의 7가지 경우 중 하나에는 무조건 속하게 된다.

최종 파일 한 개는 바로 직전 과정에서 두 개의 파일을 하나로 합쳐서 한 개가 되었을 것이다.
각 두 개 파일은 (어떤 순서로 합쳤는지는 일단 신경쓰지 않는다) 위 그림에서처럼 초록색으로 칠한 부분과 하늘색으로 칠한 부분에 해당한다.
중간에 (1, 21, 3) (4, 5, 35, 5, 4)로 나눈 부분을 답이라고 가정해보자.
그럼 위 케이스는 또 아래처럼 나눌 수 있다.
큰 문제를 작은 문제로 쪼개다가 언제 멈춰야 할까? 즉 재귀함수의 base condition을 어떻게 정의해야 할까?
수열의 길이가 2 이하가 되면 파일을 합치는 경우의 수는 한 가지밖에 없다(2개이면 2개를 하나로 합치거나, 1개는 그대로 내버려둔다). 이게 base condition이 됨을 알 수 있다.
4) dp 배열 정보를 명확히 설정한다.
- 핵심 정보는 1) 파일을 합하기 시작하는 위치 2) 합을 끝내는 위치
- 구하고자 하는 건 파일 합치는 데 드는 최소 비용이다.
- 따라서, 'dp[i][j] = V -> i번째부터 j번째까지의 파일을 합쳤을 때 드는 최소 비용' 으로 설정해서 업데이트한다.
재귀+DP를 이용한 풀이
import sys
input = sys.stdin.readline
from itertools import accumulate
def dfs(start, end):
if end - start == 1:
dp[start][end] = numbers[start] + numbers[end]
return
if end == start:
return
for i in range(start, end):
# dp[n][k] -> 이면 n번째 이상 k번째 이하의 수열, 즉 모두 포함관계
if dp[start][i] == 0:
dfs(start, i)
if dp[i+1][end] == 0:
dfs(i+1, end)
if dp[start][end] == 0 or dp[start][end] > dp[start][i] + dp[i+1][end]:
dp[start][end] = dp[start][i] + dp[i+1][end]
dp[start][end] += (acc_sum[end+1] - acc_sum[start])
return
T = int(input())
for t in range(T):
K = int(input())
numbers = list(map(int, input().split()))
acc_sum = [0] + list(accumulate(numbers))
dp = [[0]*K for _ in range(K)]
dfs(0, K-1)
print(dp[0][K-1])
꼭 모든 풀이가 100% 재귀 또는 100% dynamic programming(반복문만 활용한 bottom-up 방식)로 엄격히 구분되는 게 아니다.
재귀를 이용하면서 dynamic programming 방법을 활용하여 불필요한 연산을 줄일 수 있다.
여기선 dp 배열의 초기값을 0으로 설정한다. 각 파일 값은 양의 정수라 했으므로 아무리 파일 크기가 작아도 합하면 0보다 크기 때문이다.
만약 현재 dp 배열 값이 0이면 해당 값이 업데이트되지 않았다는 뜻이므로 재귀함수를 실행하고,
dp 배열 값이 0보다 크면 불필요한 연산을 수행하지 않고 이미 dp 배열에 저장된 값을 그대로 불러오면 된다.
# dp[x][y] 값이 0일 때만 dfs -> 재귀함수 실행
# dp[x][y] 값이 0이 아니면 if문을 건너뛰고 아래 코드를 그대로 실행
if dp[start][i] == 0:
dfs(start, i)
if dp[i+1][end] == 0:
dfs(i+1, end)
bottom-up 방식의 풀이
import sys
input = sys.stdin.readline
from itertools import accumulate
T = int(input())
for t in range(T):
K = int(input())
numbers = list(map(int, input().split()))
dp = [[0]*K for _ in range(K)]
for i in range(K-1):
dp[i][i+1] = numbers[i] + numbers[i+1]
acc_sum = [0] + list(accumulate(numbers))
for j in range(2, K):
for k in range(j-2, -1, -1):
for m in range(k, j):
if dp[k][j] == 0 or dp[k][j] > dp[k][m] + dp[m+1][j]:
dp[k][j] = dp[k][m] + dp[m+1][j]
dp[k][j] += acc_sum[j+1] - acc_sum[k]
# dp[k][j] += sum(numbers[k+1:j+1])와 동일, but 시간복잡도가 더 클 것
print(dp[0][-1])
이건 bottom-up 방식이다. 물론 재귀함수를 활용한 풀이보다 시간도 적게 걸리고 효율적이지만, 코드를 처음 마주했을 때 더 직관적으로 와닿는 건 재귀 방식의 풀이가 아닌가싶다.
백준 1520번: 내리막 길
1520번은 그래프 탐색과 DP가 결합된 문제다. 마찬가지로 top-down 방식을 떠올리면 쉽게 풀 수 있다.

DP 배열의 정의
언제나 최우선으로 해야 하는 게 DP 배열의 차원, 크기, 담긴 값의 의미를 정의 내리는 것이다.
DP 문제를 풀 때는 다소 귀찮더라도 dp 배열을 초기화한 코드 위에 주석으로 직접 설명을 써놓자.
특히 DP 차원이 늘어날수록 스스로 코드를 작성하면서도 헷갈릴 수가 있는데, 이 주석이 헷갈리는 걸 방지하는 데 크게 도움이 된다.
여기선 DP 배열을 정의하기가 쉬웠다.
(i, j) 번째 칸에서 (N-1, M-1)까지 이동할 수 있는 경로의 개수를 DP 배열에 저장하면 된다.
dp[i][j] = k: (i번째 행, j번째 열의 칸에서 이동할 수 있는 경로의 개수)
재귀와 DP를 활용한 풀이
import sys
input = sys.stdin.readline
H, W = map(int, input().split())
board = [list(map(int, input().split())) for _ in range(H)]
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
dp = [[-1]*W for _ in range(H)]
def dfs(x, y):
if x == H-1 and y == W-1:
return 1
if dp[x][y] >= 0:
return dp[x][y]
elif dp[x][y] == -1:
dp[x][y] = 0
for i in range(4):
mx, my = x+dx[i], y+dy[i]
if (0 <= mx < H and 0 <= my < W) and board[mx][my] < board[x][y]:
dp[x][y] += dfs(mx, my)
return dp[x][y]
print(dfs(0, 0))
참고로 저기서 dp[x][y]의 초기값을 -1로 설정하되 탐색을 한번 마치면 0으로 설정하는 게 굉장히 중요하다.
이 문제에선 한번 탐색을 수행한 칸이라 하더라도 다시 탐색해야 할 여지가 있고
따라서 단순하게 BFS처럼 방문했다면 다시는 방문하지 않는다면 탐색 과정에 오류가 생기게 된다.
반면에 한번 탐색을 마친 칸인데도 동일한 탐색 및 업데이트 과정을 또 거친다면 중복된(불필요한) 연산이 발생한다.
이 과정을 DP가 해결해준다.
순수하게 재귀를 이용한 풀이는 어떨까? 아래 코드를 살펴보자.
재귀만을 이용한 풀이 (시간 초과 발생)
import sys
input = sys.stdin.readline
H, W = map(int, input().split())
board = [list(map(int, input().split())) for _ in range(H)]
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
visited = [[False]*W for _ in range(H)]
def solution(x, y):
if x == H-1 and y == W-1:
return 1
answer = 0
for i in range(4):
mx, my = x+dx[i], y+dy[i]
if (0 <= mx < H and 0 <= my < W) and board[mx][my] < board[x][y] and not visited[mx][my]:
visited[mx][my] = True
cur_cnt = solution(mx, my)
visited[mx][my] = False
if cur_cnt != -1:
if answer == -1:
answer = cur_cnt
else:
answer += cur_cnt
return answer
visited[0][0] = True
print(solution(0, 0))
재귀함수를 실행하기 전에 현재 탐색하고자 하는 칸 (mx, my)는 전역변수 배열 visited를 활용해서 방문 처리해주었고,
다시 탐색해야 하기 때문에 해당 칸의 방문 여부를 다시 False로 설정했다.
이렇게 되면 탐색했던 칸을 또 탐색하고, 계속 탐색하는 불필요한 연산이 무수히 발생한다.
실제로 저 코드를 그대로 제출하면 시간 초과가 발생할 것이다.
백준 1937번: 욕심쟁이 판다
위 1520번 문제와 비슷하지만 문제 설정이 약간 다른 문제다.
1520번에서는 (0, 0)에서 (N-1, M-1)까지, 출발지와 목적지가 각각 하나로 정해져 있었고
1937번은 모든 칸에서 출발할 수 있고, 모든 칸에서 멈출 수 있다.
비유하자면 1520번은 Dijkstra's Algorithm의 성격을 띠고 있고
1937번은 Floyd-Warshall Algorithm에 가깝다고 보면 된다.
마찬가지로 dp 배열은 각 칸 (i, j)에서 방문할 수 있는 칸의 최대 개수를 담으면 된다.
여기서 구하고자 하는 건 이동할 수 있는 경로의 개수가 아니라 방문할 수 있는 칸의 개수라는 사실에 유의하자.
나는 dp 배열의 초기값을 -1로 설정한 후,
- 값이 -1이라면 아직 탐색하지 않은 칸이므로 -> 탐색 시작(재귀 실행). 값이 -1보다 크다면 탐색 X
- 현재 칸에서 이동할 수 있는 칸(상,하,좌,우)의 dp 배열 값(방문 가능 칸 수)과 비교하여 현재 칸을 업데이트
- 현재 칸에서 이동할 수 있는 칸이 아예 없다면 막다른 칸 -> 값을 1로 설정
와 같이 크게 3가지에 초점을 맞추어 코드를 작성했다.
참고로 현재 칸에서 이동할 수 있는 칸이 없다면, 자기 자신만 방문할 수 있다는 뜻이기 때문에 방문할 수 있는 칸의 개수가 1이 된다.
DP + 재귀함수를 활용한 풀이
import sys
input = sys.stdin.readline
sys.setrecursionlimit(250000)
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
def search(x, y):
is_deadend = True
cur_cnt = dp[x][y]
for i in range(4):
mx, my = x+dx[i], y+dy[i]
if 0 <= mx < N and 0 <= my < N and board[x][y] < board[mx][my]:
if dp[mx][my] == -1:
search(mx, my)
cur_cnt = max(cur_cnt, dp[mx][my])
is_deadend = False
if is_deadend:
dp[x][y] = 1
else:
if dp[x][y] == -1 or dp[x][y] < cur_cnt:
dp[x][y] = cur_cnt+1
N = int(input())
board = [list(map(int, input().split())) for _ in range(N)]
dp = [[-1]*N for _ in range(N)]
for i in range(N):
for j in range(N):
if dp[i][j] != -1:
continue
search(i, j)
print(max(max(row) for row in dp))
'알고리즘과 자료구조 > Dynamic Programming' 카테고리의 다른 글
| Dynamic Programming 5: DP 배열 설정의 중요성 (백준 14238, 17404, 12969번) (0) | 2023.04.03 |
|---|---|
| Dynamic Programming 5: DP 배열 설정의 중요성 (백준 14238, 17404, 12969번 파이썬) (0) | 2023.03.29 |
| Dynamic Programming 4: 배낭 문제 (백준 7579, 2629번 파이썬) (0) | 2023.03.29 |
| Dynamic Programming 3: 재귀(top-down)를 이용한 풀이 (백준 11049번 파이썬) (0) | 2023.03.29 |
| Dynamic Programming 1: 기초 풀이 접근 (백준 10942, 17070번) (0) | 2023.03.28 |
